Ground flow formula (Water Overlay): Difference between revisions

Latest revision as of 13:29, 5 March 2024

Ground flow is different from surface flow, since it has to account for the slowdown and porousness of the medium. In general, horizontal ground flow is calculated using formulas described in Harbaugh 2005^[1]^[2]. However, when an aquifer is present, the Aquifer formula is applied.

It depends on the configuration of the HYDRAULIC_CONDUCTIVITY_WITH_THICKNESS attribute value in the Water Overlay what Hydraulic Conductivity formula is used:

A value $<=0$ means Hydraulic Conductivity without Thickness formula will be used.
A value $>0$ means Hydraulic Conductivity with Thickness formula will be used.

Hydraulic Conductivity without Thickness

Two adjacent cells, where ground water level of cell 1 is larger than cell 2.

The flow between the two cells is calculated as:

$\Delta w_{t}=w_{1,t}-w_{2,t}$

$B_{bb}=max(B_{1}-d_{b,1},B_{2}-d_{b,2})$

$A_{c,t}=\Delta x\cdot ({\bar {w_{t}}}-B_{bb})$

$K=min(K_{1},K_{2})$

$V_{K,t}={\frac {\Delta w\cdot K\cdot A_{c,t}}{\Delta x}}\cdot \Delta t$

where:

w_{n,t}

= The ground water level of cell

n

at time

t

.

B_{c}

= the datum height of the surface of cell c, set by the elevation or a Terrain elevation prequel.

d_{b,c}

= The ground bottom distance of the cell c, defined by a Bottom distance prequel or a general GROUND_BOTTOM_DISTANCE_M of the Water Overlay.

B_{bb}

= the datum height of the bottom boundary at the edge of interaction between the two cells.

K_{n}

= The hydraulic conductivity of the cell, defined in HYDRAULIC_CONDUCTIVITY_MD of the ground terrain.

A_{c,t}

= Area of conductance at time

t

.

\Delta w

= Ground water level difference at time

t

.

\Delta t

= Computational timestep in seconds.

\Delta x

= Size of grid cell.

{\bar {w_{t}}}

= Averaged ground water level at time

t

, based on water levels in ground, WATER_STORAGE_PERCENTAGE and potentially the surface water level, when the ground is filled to the top.

V_{K,t}

= The amount of water to be transported at time

t

between one cell and the other.

Hydraulic Conductivity with Thickness

The flow between the two cells is calculated as:

$\Delta w_{t}=w_{1,t}-w_{2,t}$

$KD=min(KD_{1},KD_{2})$

$V_{KD,t}={\frac {\Delta w\cdot KD\cdot \Delta x}{\Delta x}}\cdot \Delta t$

where:

w_{n,t}

= The ground water level of cell

n

at time

t

.

KD_{n}

= The hydraulic conductivity of the cell, multiplied with the thickness of the layer, defined in HYDRAULIC_CONDUCTIVITY_WITH_THICKNESS_MD of the ground terrain.

\Delta w

= Ground water level difference at time

t

.

\Delta t

= Computational timestep in seconds.

\Delta x

= Size of grid cell.

V_{KD,t}

= The amount of water to be transported at time

t

between one cell and the other.

Aquifer formula

When an aquifer is present, its hydraulic diffusivity is used to calculate the water flow.

Based on conditions being true, the calculated volume of water that is transported through the aquifer is calculated as:

V_{a,t}={\begin{cases}{\dfrac {\Delta w_{t}\cdot {KD}_{a}\cdot \Delta x}{\Delta x}}\cdot \Delta t&{\text{if }}w_{n,t}>z_{a}{\text{ and }}KD_{a}>0\\V_{K(D),t}&{\text{otherwise}}\end{cases}}

Where:

\Delta w_{t}

= Ground water level difference between the two adjacent cells at time

t

;

{KD}_{a}

= The AQUIFER_KD attribute of aquifer.

\Delta x

= Size of grid cell.

\Delta t

= Computational timestep in seconds.

w_{n,t}

= Ground water level in cell

n

at time

t

;

z_{a}

= the datum height of the aquifer at the cell.

V_{K(D),t}

= The calculated amount of water to be transported at time

t

between one cell and the other.

V_{a,t}

= Volume in

m^{3}

that flows between the two adjacent cells due to the aquifer at time

t

.

References

↑ Harbaugh, A.W., 2005, MODFLOW-2005, the U.S. Geological Survey modular ground-water model-the Ground-Water Flow Process: U.S. Geological Survey Techniques and Methods 6-A16, variously paginated.
↑ Langevin, C.D., Hughes, J.D., Banta, E.R., Niswonger, R.G., Panday, Sorab, and Provost, A.M. (2017) ∙ Documentation for the MODFLOW 6 Groundwater Flow Model: U.S. Geological Survey Techniques and Methods, book 6, chap. A55 ∙ p 31 ∙ found at: https://doi.org/10.3133/tm6A55 (last visited 2019-02-04)

Models

Surface • Ground • Rain • Evaporation • Infiltration • Elevation • Breach • Sewer • Storage • Tracer flow • Border • Order
Model formulas

Timestep • Season • Surface water level • Groundwater level
Flow formulas

Surface flow • Surface infiltration • Ground flow • Ground infiltration • Surface evaporation • Ground evaporation • Ground bottom flow
Hydraulic structure formulas

Culvert • Weir • Breach growth • Breach flow • Pump • Sewer Overflow • Inlet • Drainage
Related

Building attributes • Hydrological features • Hydraulic structures • Terrain attributes • Model attributes • Results • Simulation data

[Harbaugh-1] Harbaugh, A.W., 2005, MODFLOW-2005, the U.S. Geological Survey modular ground-water model-the Ground-Water Flow Process: U.S. Geological Survey Techniques and Methods 6-A16, variously paginated.

[Modflow-2] Langevin, C.D., Hughes, J.D., Banta, E.R., Niswonger, R.G., Panday, Sorab, and Provost, A.M. (2017) ∙ Documentation for the MODFLOW 6 Groundwater Flow Model: U.S. Geological Survey Techniques and Methods, book 6, chap. A55 ∙ p 31 ∙ found at: https://doi.org/10.3133/tm6A55 (last visited 2019-02-04)

[1]

[2]

@@ Line 1: / Line 1: @@
-Underground flow is calculated differently from surface flow, to account for the slowdown and porousness of the medium.
+Ground flow is different from surface flow, since it has to account for the slowdown and porousness of the medium. In general, horizontal ground flow is calculated using formulas described in Harbaugh 2005<ref name="Harbaugh"/><ref name="Modflow"/>. However, when an [[Aquifer (Water_Overlay)|aquifer]] is present, the [[ground flow formula (Water Overlay)#Aquifer formula|Aquifer formula]] is applied.
-In general, Darcy's law is used. When an {{inlink|lcase=1|aquifer}} is present a variant is applied.
+It depends on the configuration of the [[Hydraulic conductivity with thickness (Water Overlay)|HYDRAULIC_CONDUCTIVITY_WITH_THICKNESS]] attribute value in the [[Water Overlay]] what Hydraulic Conductivity formula is used:
+* A value <math><= 0</math> means [[Ground flow formula (Water Overlay)#Hydraulic Conductivity without Thickness|Hydraulic Conductivity without Thickness]] formula will be used.
+* A value <math>> 0</math> means [[Ground flow formula (Water Overlay)#Hydraulic Conductivity with Thickness|Hydraulic Conductivity with Thickness]] formula will be used.
+===Hydraulic Conductivity without Thickness===
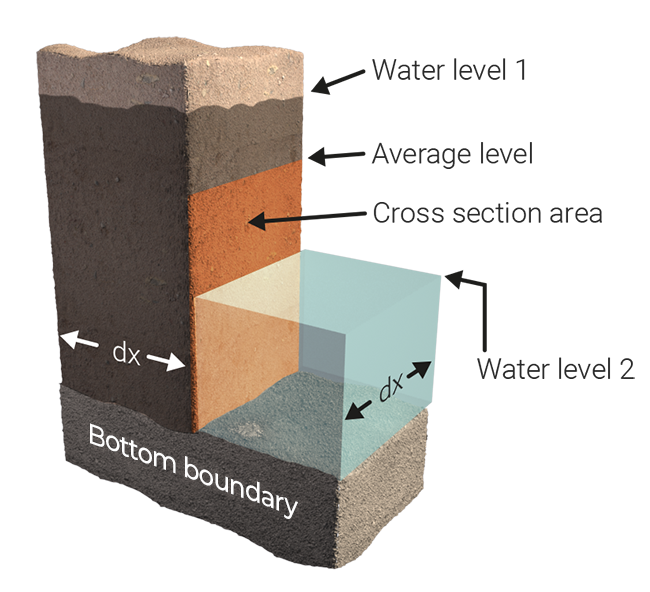
+[[File:Undergroundflow2.png|right|400px|thumb|Two adjacent cells, where ground water level of cell 1 is larger than cell 2.]]
+The flow between the two cells is calculated as:
-=====Darcy's law=====
+<math>\Delta w_t = w_{1,t} - w_{2,t}</math>
-Underground flow between cells is calculated using Darcy's law<ref name="Modflow"/>.
-: ''C<sub>d</sub> = Δt * I<sub>und</sub> * width * A * ( (WL<sub>source</sub> - WL<sub>target</sub>) / distance )
+<math>B_{bb} = max ( B_{1}- d_{b,1} , B_{2}- d_{b,2} ) </math>
-Since both ''width'' and ''distance'' are directly related to the cell size, and the result should be in water height rather than volume, the formula can be rewritten as follows:
+<math>A_{c,t} = \Delta x \cdot ( \bar{w_{t}} - B_{bb} )</math>
-: ''C<sub>d</sub> = Δt * I<sub>und</sub> * A * (W<sub>source</sub> - W<sub>target</sub>) / cell
+<math>K = min(K_{1} , K_{2} )</math>
-Because the underground may have a different porousness, the maximum amount of water that can flow to another cell has to take into account the relative water storage capacities of the underground.
+<math>V_{K,t} = \frac{\Delta w \cdot K \cdot A_{c,t}}{ \Delta x} \cdot \Delta t</math>
-: ''C<sub>wsp</sub> = (WL<sub>source</sub> - WL<sub>target</sub>) * (WSP<sub>source</sub> / (WSP<sub>source</sub> + WSP<sub>target</sub>) )
+where:
+: <math>w_{n,t}</math> = The [[Groundwater level formula (Water Overlay)|ground water level]] of cell <math>n</math> at time <math>t</math>.
+: <math>B_c</math> = the datum height of the surface of cell c, set by the [[Elevation (Water Overlay)|elevation]] or a [[Terrain elevation prequel (Water Overlay)|Terrain elevation prequel]].
+: <math>d_{b,c}</math> = The ground bottom distance of the cell c, defined by a [[Bottom distance prequel (Water Overlay)|Bottom distance prequel]] or a general [[Ground_bottom_distance_m_(Water_Overlay)|GROUND_BOTTOM_DISTANCE_M]] of the Water Overlay.
+: <math>B_{bb}</math> = the datum height of the bottom boundary at the edge of interaction between the two cells.
+: <math>K_n</math> = The hydraulic conductivity of the cell, defined in [[Terrain hydraulic conductivity md (Water Overlay)|HYDRAULIC_CONDUCTIVITY_MD]] of the ground terrain.
+: <math>A_{c,t}</math> = Area of conductance at time <math>t</math>.
+: <math>\Delta w</math> = Ground water level difference at time <math>t</math>.
+: <math>\Delta t</math> = Computational [[Timestep formula (Water Overlay)|timestep]] in seconds.
+: <math>\Delta x</math> = Size of grid cell.
+: <math>\bar{w_{t}}</math> = Averaged ground water level at time <math>t</math>, based on water levels in ground, [[Terrain water storage percentage (Water Overlay)|WATER_STORAGE_PERCENTAGE]] and potentially the [[Surface water level formula (Water Overlay)|surface water level]], when the ground is filled to the top.
+: <math>V_{K,t}</math> = The amount of water to be transported at time <math>t</math> between one cell and the other.
+<br clear=both>
-The amount of water which flows from the source to the target cell is calculated as follows:
+===Hydraulic Conductivity with Thickness===
+The flow between the two cells is calculated as:
-: ''Δw = max( 0 , min( C<sub>d</sub> , C<sub>wsp</sub> ) )
+<math>\Delta w_t = w_{1,t} - w_{2,t}</math>
-Where:
+<math>KD = min(KD_{1} , KD_{2} )</math>
-* Δw = The underground flow which takes place.
-* Δt = Computational timestep.
-* cell = Cell size.
-* C<sub>d</sub> = The capacity for water flow possible based on the relative water heights.
+<math>V_{KD,t} = \frac{\Delta w \cdot KD \cdot \Delta x }{ \Delta x} \cdot \Delta t</math>
-* C<sub>wsp</sub> = The capacity for water flow possible based on the relative water storage percentages.
-* WL<sub>source</sub> = The amount of water in the saturated zone of the source cell. The height of the water column if the equivalent amount of water was placed on the surface.
+where:
-* WL<sub>target</sub> = The amount of water in the saturated zone of the target cell. The height of the water column if the equivalent amount of water was placed on the surface.
+: <math>w_{n,t}</math> = The [[Groundwater level formula (Water Overlay)|ground water level]] of cell <math>n</math> at time <math>t</math>.
-* A = Contact area of the underground cells
+: <math>KD_n</math> = The hydraulic conductivity of the cell, multiplied with the thickness of the layer, defined in [[Terrain hydraulic conductivity with thickness md (Water Overlay)|HYDRAULIC_CONDUCTIVITY_WITH_THICKNESS_MD]] of the ground terrain.
-* I<sub>und</sub> = The [[Ground infiltration md (Terrain) (Water Overlay)|GROUND_INFILTRATION_MD]] of the underground terrain type of the origin cell.
+: <math>\Delta w</math> = Ground water level difference at time <math>t</math>.
-* WSP<sub>source</sub> = The [[Water storage percentage (Terrain) (Water Overlay)|WATER_STORAGE_PERCENTAGE]] of the underground terrain type of the origin cell.
+: <math>\Delta t</math> = Computational [[Timestep formula (Water Overlay)|timestep]] in seconds.
-* WSP<sub>target</sub> = The WATER_STORAGE_PERCENTAGE of the underground terrain type of the target cell.
+: <math>\Delta x</math> = Size of grid cell.
+: <math>V_{KD,t}</math> = The amount of water to be transported at time <math>t</math> between one cell and the other.
-=====Aquifer formula=====
+===Aquifer formula===
-When an aquifer is present, its hydraulic diffusivity is used to calculate the water flow.
+When an [[Aquifer (Water_Overlay)|aquifer]] is present, its [[Aquifer kd (Water Overlay)|hydraulic diffusivity]] is used to calculate the water flow.
-First, the hydraulic diffusivity dictates the fraction of the water height difference which will flow.
+Based on conditions being true, the calculated volume of water that is transported through the aquifer is calculated as:
-: ''F = 2 * sqrt( KD / WSP<sub>source</sub> ) * sqrt( Δt ) * ( 1 / cell )''
+: <math>V_{a,t} =
+\begin{cases}
-Based on this fraction, the actual amount of water flow is calculated.
+ \dfrac{ \Delta w_{t} \cdot {KD}_a \cdot \Delta x}{\Delta x} \cdot \Delta t & \text{if } w_{n,t} > z_a  \text{ and } KD_a > 0 \\
-: ''Δw = ( (WL<sub>source</sub>/WSP<sub>source</sub>) - (WL<sub>target</sub>/WSP<sub>source</sub>) ) * F''
+ V_{K(D),t}  & \text{otherwise}
+\end{cases}
+</math>
 Where:
-* Δw = The underground flow which takes place.
+: <math>\Delta w_{t}</math> = Ground water level difference between the two adjacent cells at time <math>t</math>;
-* Δt = Computational timestep.
+: <math>{KD}_a</math> = The [[Aquifer kd (Water Overlay)|AQUIFER_KD]] attribute of aquifer.
-* cell = Cell size.
+: <math>\Delta x</math> = Size of grid cell.
+: <math>\Delta t</math> = Computational [[Timestep formula (Water Overlay)|timestep]] in seconds.
+: <math>w_{n,t}</math> = Ground water level in cell <math>n</math> at time <math>t</math>;
+: <math>z_a</math> = [[Aquifer datum (Water Overlay)|the datum height of the aquifer]] at the cell.
+: <math>V_{K(D),t}</math> = The calculated amount of water to be transported at time <math>t</math> between one cell and the other.
+: <math>V_{a,t}</math> = Volume in <math>m^{3}</math> that flows between the two adjacent cells due to the aquifer at time <math>t</math>.
-* F = Fraction of water which flows between cells
+{{article end
+|related=
-* KD = The {{inlink|AQUIFER_KD}} attribute of aquifer.
+The following topics are related to this formula.
-* WSP<sub>source</sub> = The {{inlink|WATER_STORAGE_PERCENTAGE}} attribute of the underground terrain type of the origin cell.
+; Features
-* WSP<sub>target</sub> = The {{inlink|WATER_STORAGE_PERCENTAGE}} attribute of the underground terrain type of the target cell.
+: [[Aquifer (Water Overlay)]]
-* WL<sub>source</sub> = The amount of water in the saturated zone of the source cell. The height of the water column if the equivalent amount of water was placed on the surface.
+; Formulas
-* WL<sub>target</sub> = The amount of water in the saturated zone of the target cell. The height of the water column if the equivalent amount of water was placed on the surface.
+: [[Groundwater level formula (Water Overlay)]]
+: [[Ground infiltration formula (Water Overlay)]]
-==References==
+; Models
+: [[Ground model (Water Overlay)]]
+: [[Infiltration model (Water Overlay)]]
+: [[Tracer flow model (Water Overlay)]]
+|seealso=
+* [[Ground model (Water Overlay)#Horizontal flow and aquifers| Ground model]]
+|references=
 <references>
-<ref name="Modflow">Langevin, C.D., Hughes, J.D., Banta, E.R., Niswonger, R.G., Panday, Sorab, and Provost, A.M. (2017) ∙ Documentation
+<ref name="Modflow">Langevin, C.D., Hughes, J.D., Banta, E.R., Niswonger, R.G., Panday, Sorab, and Provost, A.M. (2017) ∙ Documentation for the MODFLOW 6 Groundwater Flow Model: U.S. Geological Survey Techniques and Methods, book 6, chap. A55 ∙ p 31 ∙ found at:  https://doi.org/10.3133/tm6A55 (last visited 2019-02-04)</ref>
-for the MODFLOW 6 Groundwater Flow Model: U.S. Geological Survey Techniques and Methods, book 6, chap. A55 ∙ p 31 ∙ found at:  https://doi.org/10.3133/tm6A55 (last visited 2019-02-04)</ref>
+<ref name="Harbaugh">Harbaugh, A.W., 2005, MODFLOW-2005, the U.S. Geological Survey modular ground-water model-the Ground-Water Flow Process: U.S. Geological Survey Techniques and Methods 6-A16, variously paginated.</ref>
 </references>
-{{Template:WaterOverlay_nav}}
+}}
+{{WaterOverlay formula nav}}

Ground flow formula (Water Overlay): Difference between revisions

Latest revision as of 13:29, 5 March 2024

Contents

Hydraulic Conductivity without Thickness

Hydraulic Conductivity with Thickness

Aquifer formula

Related

See also

References

Navigation menu

Ground flow formula (Water Overlay): Difference between revisions

Latest revision as of 13:29, 5 March 2024

Hydraulic Conductivity without Thickness

Hydraulic Conductivity with Thickness

Aquifer formula

Related

See also

References

Navigation menu

Search