Elevation model (Water Overlay)

The elevation model is determined using two steps:

Rasterization of the height sectors and buildings
Piecewise linear reconstruction of the bottom

Rasterization of height points of height sectors and buildings

The base land height values can originate from two sources:

The height sectors and additional actions (levees
A Terrain elevation prequel

Often the height source has more height values for a particular grid cell. The calculate height value for that grid cell is then calculated as the average of these points.

Added to the rasterized land height are the building heights. A building's height is calculated based on the floor height times the amount of floors, slanting roof height and optional height offset. In case a building has a Custom Geometry, the height is calculated based on this custom geometry, within the boundaries of the grid cell, with the addition of the optional height offset.

How bridges are handled as buildings depend on the configured bridge mode.

These buildings heights (including bridges!) are limited by the design flood elevation and the height taken is whichever is lowest.

Furthermore certain conditions, such as a configured Weir Height or Culvert Threshold can override a grid cell elevation. This overriding also provides a preference for the piecewise linear reconstruction.

Piecewise linear reconstruction of the bottom

The implementation of the Water Module is based on second-order semi-discrete central-upwind scheme by Kurganov and Petrova (2007)^[1]. The surface elevation, also named bottom in the paper, is slightly adjusted to support the scheme to become well balanced and positivity preserving. The process of adjusting the original surface elevation is called piecewise linear reconstruction of the bottom.

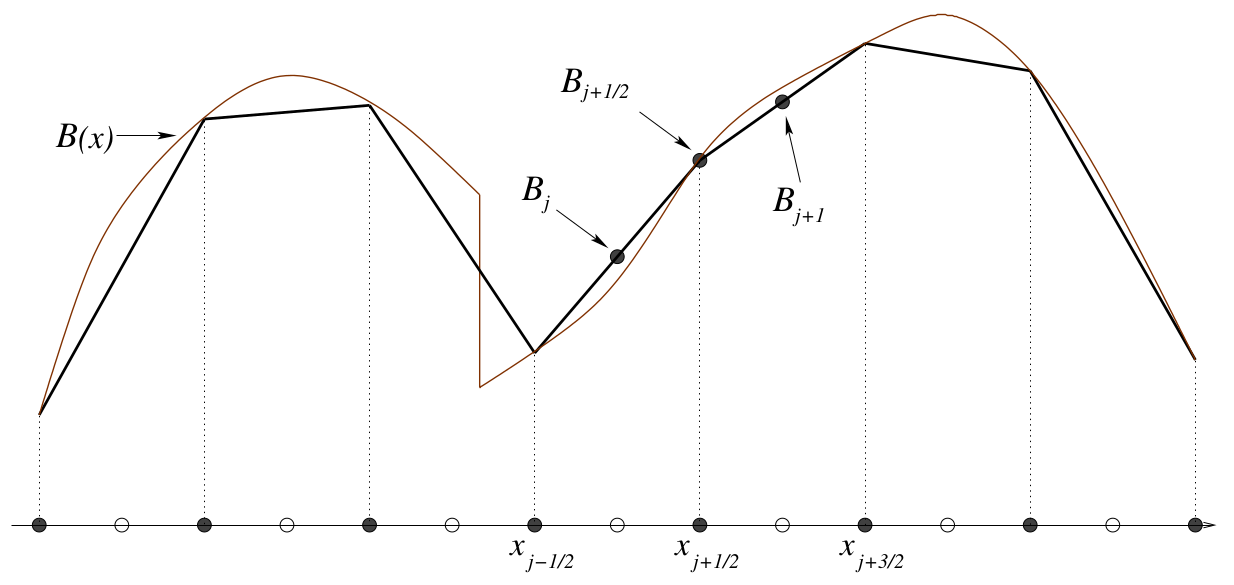
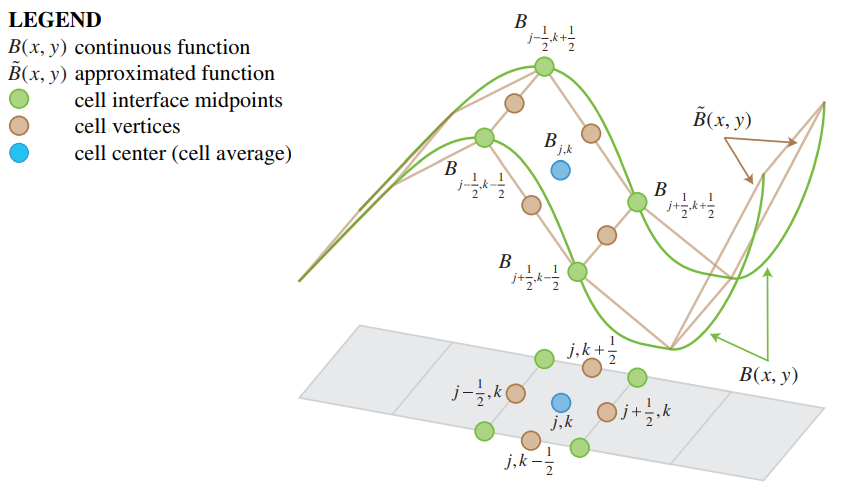
1D linear piecewise reconstruction. Source: Kurganov and Petrova (2007)^[1]

The first requirement the scheme to become well balanced and positivity preserving is to ensure that each grid cell has a constant linear slope in both the x- and y- direction. Secondly the end points of the slope should meet in the center of the cell's edges. This ensures that the bottom is continuous along cells in the x- and y- direction. Thirdly, the linear slope in the x- and y-direction within a cell should meet in a single center point.

To fulfill these requirements, the following steps are taken:

Pick or calculate the height points for the 4 corners of the cell. A height point is picked when an override height is provided, such as a Weir Height.
Form a rectangle with the 4 corners and calculate the centers of these edges. (These are the points that have to meet for continuity)
Calculate a new center point based on the 4 edge center points.

Given that the adjacent cells share the same corner points, and thus share an edge center point, the bottom will be continuous in the x and y direction. Furthermore, the cell has an linear slope in both the x- and y-direction. The only downside is that the new center point might have been placed heigher or lower in a situation where the terrain's slope was originally not linear within the cell.

2D linear piecewise reconstruction. Source: Horváth et al. (2014)^[2]
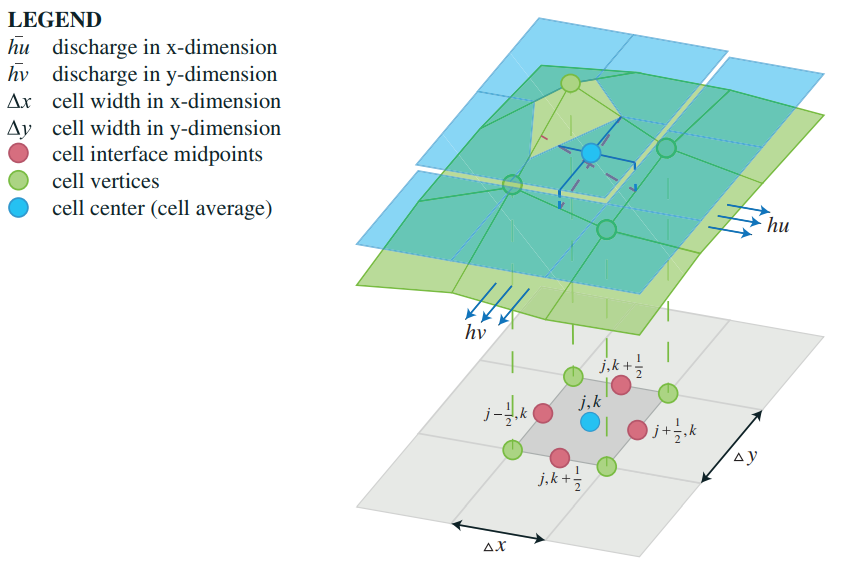
Application of reconstructed elevation Source: Horváth et al. (2014)^[2]

Notes

An alternative elevation model can be provided as a prequel.
The smaller the grid size, the closer the bottom reconstruction will approximate the original surface elevation.
The resulting elevation model can be inspected in a project using the SURFACE_ELEVATION result type.

References

↑ ^1.0 ^1.1 Kurganov A, Petrova G (2007) ∙ A Second-Order Well-Balanced Positivity Preserving Central-Upwind Scheme for the Saint-Venant System ∙ found at: http://www.math.tamu.edu/~gpetrova/KPSV.pdf (last visited 2018-06-29)
↑ ^2.0 ^2.1 Zsolt Horváth, Jürgen Waser, Rui A. P. Perdigão, Artem Konev and Günter Blöschl (2014) ∙ A two-dimensional numerical scheme of dry/wet fronts for the Saint-Venant system of shallow water equations ∙ found at: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.700.7977&rep=rep1&type=pdf ∙ http://visdom.at/media/pdf/publications/Poster.pdf ∙ (last visited 2018-06-29)