Breach growth formula (Water Overlay)
Water can flow through breaches into levee protected areas. These breaches often start small and grow over time.
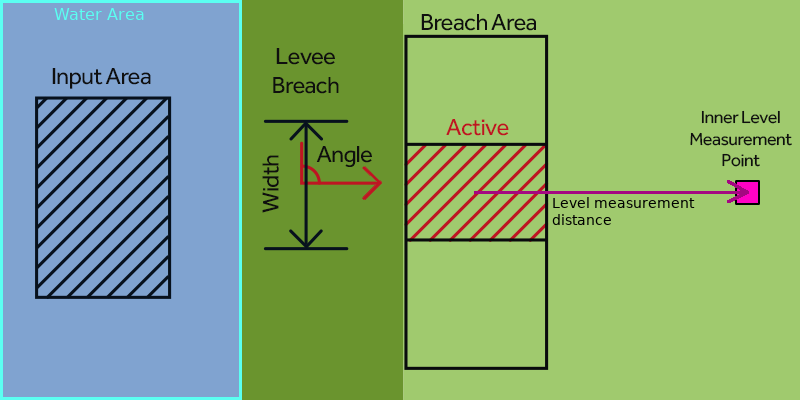
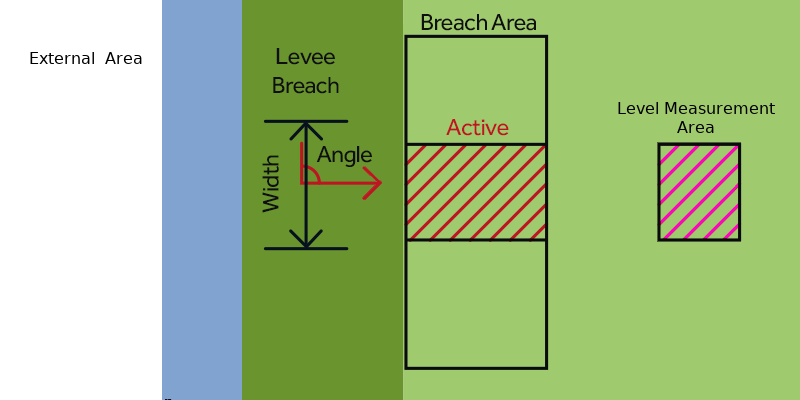
The water flowing through breaches can originate from an external area outside the project area or an input area within the project area.
This algorithm is based on the incremental timestep formula of Verheij-van der Knaap[1], as described in section 3.4.4 Implementatie in SOBEK and the conclusion of that paper.
First, the difference in height of the water on either side of the breach is calculated.
Using the height difference, the breach width increase (m/s) is calculated per computational timestep.
The current breach width is then equal to the last calculated breach width, plus the calculated breach width increment.
Where:
- = The BREACH_WIDTH of the breach.
- = The BREACH_HEIGHT (datum) of the breach at time t.
- = The calculated breach width, initially equal to .
- = Inner water level at breach area at time t, measured at the measurement point (or Level Area) of the Breach.
- = Outer water level at Input Area (or external area) at time t.
- = The difference between the height of the water columns on either side of the breach at time t.
- = Material factor, set to 1.3 (average for sand and clay levees).
- = Constant, set to 0.04.
- = the acceleration due to gravity, set to 9.80665.
- = The critical BREACH_SPEED of the breach (e.g. 0.2 for sand and 0.5 for clay).
- = The calculated width increase of the breach at time t.
- = Computational timestep.
Notes
- The breach height Hb,t can be defined over time, by configuring the BREACH_HEIGHT as an attribute array.
- The inner water level is to be measured not directly inside the breach area but a few meters away. By default 100m, this can be adjusted via the BREACH_MEASUREMENT_DISTANCE_M attribute. It can also be measured using a manual defined level area.
- For more details on breach growth, we also recommend reading this "Quickscan"-report for Waterschap Rijn en IJssel[2].
How-to's
Related
The following topics are related to this formula.
- Features
- Breach
- Formulas
- Breach flow formula
- Models
- Breach Model
- Surface model
See also
For an example of the breach growth, take a look at the Demo Breach Project available in all domains.
References
- ↑ Verheij, H.J. ∙ Aanpassen van het bresgroeimodel in HIS-OM: Bureaustudie ∙ found at: http://resolver.tudelft.nl/uuid:aedc8109-da43-4a03-90c3-44f706037774 ∙ (last visited 2022-09-08)
- ↑ Arcadis ∙ Quickscan Lijnvormige Kerende Elementen Onderzoek naar de modellering van bresgroei en standzekerheid van Lijnvormige Kerende Elementen Waterschap Rijn en IJssel ∙ found at: https://edepot.wur.nl/556012 ∙ (last visited 2022-09-08)