Ground flow formula (Water Overlay): Difference between revisions

From Tygron Support wiki
Jump to navigation Jump to search
Line 5: Line 5:
The flow between the two cells is calculated as:
The flow between the two cells is calculated as:


<math>\Delta w = w_{1} - w_{2}</math>
<math>\Delta w_t = w_{1,t} - w_{2,t}</math>


<math>B_{ex} = max ( B_{1} , B_{2} ) - D_{ground}</math>
<math>B_{ex} = max ( B_{1} , B_{2} ) - D_{ground}</math>


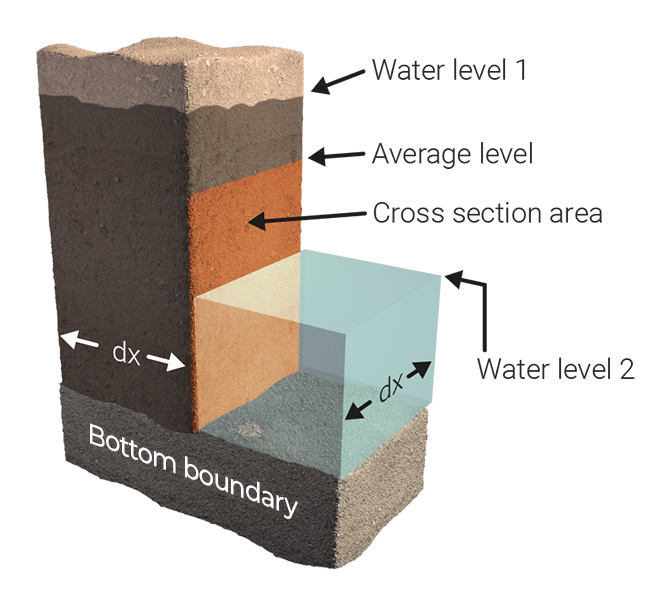
<math>A_{c} = \Delta x \cdot ( w_{avg} - B_{ex} )</math>
<math>A_{c,t} = \Delta x \cdot ( w_{avg,t} - B_{ex} )</math>


<math>K = min(K_{1} , K_{2} )</math>
<math>K = min(K_{1} , K_{2} )</math>


<math>q = \Delta w \cdot K \cdot A_{c} / \Delta x \cdot \Delta t</math>
<math>q_t = \Delta w \cdot K \cdot A_{c} / \Delta x \cdot \Delta t</math>


where:
where:
: <math>w_n</math> = The [[Groundwater level formula (Water Overlay)|underground water level]] of cell n.
: <math>w_n</math> = The [[Groundwater level formula (Water Overlay)|underground water level]] of cell <math>n</math> at time <math>t</math>.
: <math>B_n</math> = The [[terrain height (Water Overlay)|surface height]] of cell n.
: <math>B_n</math> = The [[terrain height (Water Overlay)|surface height]] of cell n.
: <math>K_n</math> = The hydraulic conductivity of the cell, defined in [[Terrain hydraulic conductivity md (Water Overlay)|HYDRAULIC_CONDUCTIVITY_MD]] of the underground terrain.
: <math>K_n</math> = The hydraulic conductivity of the cell, defined in [[Terrain hydraulic conductivity md (Water Overlay)|HYDRAULIC_CONDUCTIVITY_MD]] of the underground terrain.
: <math>D_{ground}</math> = The configured ground bottom distance, defined in [[Ground_bottom_distance_m_(Water_Overlay)|GROUND_BOTTOM_DISTANCE_M]] of the Water Overlay.  
: <math>D_{ground}</math> = The configured ground bottom distance, defined in [[Ground_bottom_distance_m_(Water_Overlay)|GROUND_BOTTOM_DISTANCE_M]] of the Water Overlay.  
: <math>A_c</math> = Area of conductance.
: <math>A_{c,t></math> = Area of conductance at time <math>t</math>..
: <math>\Delta w</math> = Underground water level difference.
: <math>\Delta w</math> = Underground water level difference.
: <math>\Delta t</math> = Computational timestep.
: <math>\Delta t</math> = Computational timestep.
: <math>\Delta x</math> = Size of grid cell.
: <math>\Delta x</math> = Size of grid cell.
: <math>w_{avg}</math> = Averaged underground water level, based on water levels in underground, [[Terrain water storage percentage (Water Overlay)|WATER_STORAGE_PERCENTAGE]] and potentially the [[Surface water level formula (Water Overlay)|surface water level]], when the underground is filled to the top.
: <math>w_{avg,t}</math> = Averaged underground water level at time <math>t</math>, based on water levels in underground, [[Terrain water storage percentage (Water Overlay)|WATER_STORAGE_PERCENTAGE]] and potentially the [[Surface water level formula (Water Overlay)|surface water level]], when the underground is filled to the top.
: <math>q_t</math> = The amount of water to be transported at time <math>t</math> between one cell and the other
<br clear=both>
<br clear=both>


Revision as of 17:26, 1 February 2023

Underground flow is different from surface flow, since it has to account for the slowdown and porousness of the medium. In general, horizontal underground flow is calculated using formulas described in Harbaugh 2005[1][2]. However, when an aquifer is present, the aquifer variant is applied.

Hydraulic Conductivity without Thickness

Two adjacent cells, where underground water level of cell 1 is larger than cell 2.

The flow between the two cells is calculated as:

where:

= The underground water level of cell at time .
= The surface height of cell n.
= The hydraulic conductivity of the cell, defined in HYDRAULIC_CONDUCTIVITY_MD of the underground terrain.
= The configured ground bottom distance, defined in GROUND_BOTTOM_DISTANCE_M of the Water Overlay.
Failed to parse (syntax error): {\displaystyle A_{c,t>} = Area of conductance at time ..
= Underground water level difference.
= Computational timestep.
= Size of grid cell.
= Averaged underground water level at time , based on water levels in underground, WATER_STORAGE_PERCENTAGE and potentially the surface water level, when the underground is filled to the top.
= The amount of water to be transported at time between one cell and the other


Aquifer formula

When an aquifer is present, its hydraulic diffusivity is used to calculate the water flow.

First the following condition is checked in order to allow water movement through the aquifer:

Based on this condition being true, the transported volume V is calculated:


Where:

= Ground water level in the cell at time ;
= the datum height of the aquifer at the cell.
= Volume in that flows between the two adjacent cells due to the aquifer.
= Ground water level difference between the two adjacent cells at time ;
= Computational timestep.
= The AQUIFER_KD attribute of aquifer.

Related

The following topics are related to this formula.

Features
Aquifer
Formulas
Groundwater level formula
Underground infiltration formula
Models
Underground model
Infiltration model
Tracer flow model

See also

References

  1. ↑ Harbaugh, A.W., 2005, MODFLOW-2005, the U.S. Geological Survey modular ground-water model-the Ground-Water Flow Process: U.S. Geological Survey Techniques and Methods 6-A16, variously paginated.
  2. ↑ Langevin, C.D., Hughes, J.D., Banta, E.R., Niswonger, R.G., Panday, Sorab, and Provost, A.M. (2017) ∙ Documentation for the MODFLOW 6 Groundwater Flow Model: U.S. Geological Survey Techniques and Methods, book 6, chap. A55 ∙ p 31 ∙ found at: https://doi.org/10.3133/tm6A55 (last visited 2019-02-04)
Water Module
Benchmarks button.png
Introduction button.png
Water Module
Benchmarks button.png
Getting started button.png
Tutorials
Benchmarks button.png
Overview button.png
Overview
Benchmarks button.png
Theory button.png
Theory
Benchmarks button.png
Benchmarks button.png
Benchmarks
Models
Surface • Ground • Rain • Evaporation • Infiltration • Elevation • Breach • Sewer • Storage • Tracer flow • Border • Order
Model formulas
Timestep • Season • Surface water level • Groundwater level
Flow formulas
Surface flow • Surface infiltration • Ground flow • Ground infiltration • Surface evaporation • Ground evaporation • Ground bottom flow
Hydraulic structure formulas
Culvert • Weir • Breach growth • Breach flow • Pump • Sewer Overflow • Inlet • Drainage
Related
Building attributes • Hydrological features • Hydraulic structures •  Terrain attributes • Model attributes • Results • Simulation data
Retrieved from "https://support.tygron.com/w/index.php?title=Ground_flow_formula_(Water_Overlay)&oldid=51156"