Elevation model (Water Overlay): Difference between revisions

From Tygron Support wiki
Jump to navigation Jump to search
 
(39 intermediate revisions by 4 users not shown)
Line 1: Line 1:
Two aspects are described on this page:
The elevation model is determined using two steps:
Rasterization of the height sectors
* Rasterization of the height sectors and buildings
Piecewise linear reconstruction of the bottom.
* Piecewise linear reconstruction of the bottom


===Rasterization of height points of height sectors and buildings===
The base land height values can originate from two sources:
* The height sectors and additional actions (levees
* A [[Terrain elevation prequel (Water Overlay)|Terrain elevation prequel]]
Often the height source has more height values for a particular grid cell. The calculate height value for that grid cell is then calculated as the average of these points.
Added to the rasterized land height are the [[building]] heights. A building's height is calculated based on the [[Floor height m (Function Value)|floor height]] times the amount of floors, [[Slanting roof height (Function Value)|slanting roof height]] and optional [[Height offset (Function Value)|height offset]]. In case a building has a [[Custom Geometry]], the height is calculated based on this custom geometry, within the boundaries of the grid cell, with the addition of the optional height offset.
How bridges are handled as buildings depend on the configured [[Bridge elevation (Water Overlay)|bridge mode]].
These buildings heights (including bridges!) are limited by the [[Design flood elevation m (Water Overlay)|design flood elevation]] and the height taken is whichever is lowest.
Furthermore certain conditions, such as a configured [[Weir height (Water Overlay)|Weir Height]] or [[Culvert threshold (Water Overlay)|Culvert Threshold]] can override a grid cell elevation. This overriding also provides a preference for the piecewise linear reconstruction.


===Piecewise linear reconstruction of the bottom===
===Piecewise linear reconstruction of the bottom===
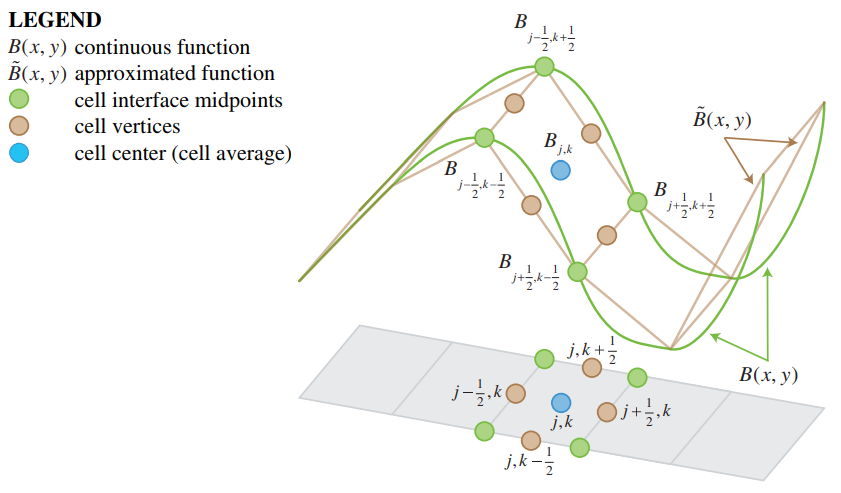
The implementation of the Water Module is based on second-order semi-discrete central-upwind scheme by Kurganov and Petrova (2007)<ref name="Kurganov2"/>
The implementation of the Water Module is based on second-order semi-discrete central-upwind scheme by Kurganov and Petrova (2007)<ref name="Kurganov2"/>. The [[terrain height (Water Overlay)|surface elevation]], also named bottom in the paper, is slightly adjusted to support the scheme to become ''well balanced and positivity preserving''. The process of adjusting the original surface elevation is called ''piecewise linear reconstruction of the bottom''.  
The surface elevation, also named bottom in the paper, is slightly adjusted which allows the scheme to become well balanced and positivity preserving.
[[File:piecewisereconstruction_1d.png|left|thumb|400px|1D linear piecewise reconstruction. Source: Kurganov and Petrova (2007)<ref name="Kurganov2" />]]{{clear}}
The process of adjusting the original surface elevation is called ''piecewise linear reconstruction of the bottom''. It works as followed:
 
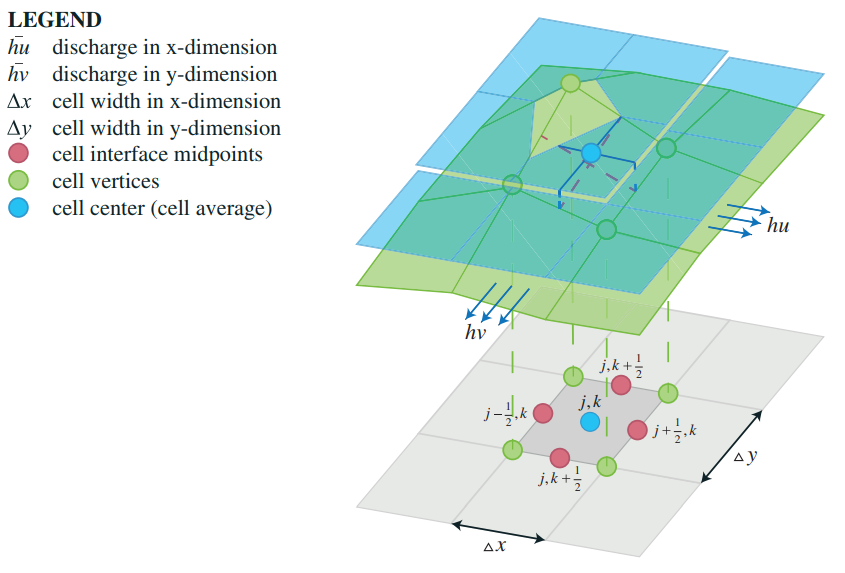
[[File:piecewisereconstruction_1d.png]]
The first requirement the scheme to become ''well balanced and positivity preserving'' is to ensure that each grid cell has a constant linear slope in both the x- and y- direction. Secondly the end points of the slope should meet in the center of the cell's edges. This ensures that the bottom is continuous along cells in the x- and y- direction. Thirdly, the linear slope in the x- and y-direction within a cell should meet in a single center point.
 
To fulfill these requirements, the following steps are taken:
# Pick or calculate the height points for the 4 corners of the cell. A height point is picked when an override height is provided, such as a Weir Height.
# Form a rectangle with the 4 corners and calculate the centers of these edges. (These are the points that have to meet for continuity)
# Calculate a new center point based on the 4 edge center points.


[[File:Inundation overlay 04 HWP(1).PNG|thumb|250px|Source: Horváth et al. (2014)<ref name="Horvath"/>]]
Given that the adjacent cells share the same corner points, and thus share an edge center point, the bottom will be continuous in the x and y direction. Furthermore, the cell has an linear slope in both the x- and y-direction. The only downside is that the new center point might have been placed heigher or lower in a situation where the terrain's slope was originally not linear within the cell.
[[File:Inundation overlay 04 HWP(2).PNG|thumb|250px|Source: Horváth et al. (2014)<ref name="Horvath"/>]]
<gallery widths=400px heights=300px>
File:Inundation overlay 04 HWP(2).PNG|2D linear piecewise reconstruction. Source: Horváth et al. (2014)<ref name="Horvath"/>
File:Inundation overlay 04 HWP(1).PNG|left|thumb|400px|Application of reconstructed elevation Source: Horváth et al. (2014)<ref name="Horvath"/>
</gallery>


==References==
{{article end
|notes=
* An [[terrain elevation prequel (Water Overlay)|alternative elevation model]] can be provided as a [[prequel]].
* The smaller the [[grid cell size|grid size]], the closer the bottom reconstruction will approximate the original [[terrain height (Water Overlay)|surface elevation]].
* The resulting elevation model can be inspected in a project using the [[Surface elevation result type (Water Overlay)|SURFACE_ELEVATION]] result type.
|seealso=
* [[Elevation (Water Overlay)]]
* [[Terrain elevation prequel (Water Overlay)]]
* [[Design flood elevation m (Water Overlay)]]
|references=
<references>
<references>
<ref name="Kurganov2">Kurganov A, Petrova G (2007) ∙ A Second-Order Well-Balanced Positivity Preserving Central-Upwind Scheme for the Saint-Venant System ∙ found at: http://www.math.tamu.edu/~gpetrova/KPSV.pdf (last visited 2018-06-29)</ref>
<ref name="Kurganov2">Kurganov A, Petrova G (2007) ∙ A Second-Order Well-Balanced Positivity Preserving Central-Upwind Scheme for the Saint-Venant System ∙ found at: http://www.math.tamu.edu/~gpetrova/KPSV.pdf (last visited 2018-06-29)</ref>
<ref name="Horvath">Zsolt Horváth, Jürgen Waser, Rui A. P. Perdigão, Artem Konev and Günter Blöschl (2014) ∙ A two-dimensional numerical scheme of dry/wet fronts for the Saint-Venant system of shallow water equations ∙ found at: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.700.7977&rep=rep1&type=pdf ∙ http://visdom.at/media/pdf/publications/Poster.pdf ∙ (last visited 2018-06-29)</ref>
<ref name="Horvath">Zsolt Horváth, Jürgen Waser, Rui A. P. Perdigão, Artem Konev and Günter Blöschl (2014) ∙ A two-dimensional numerical scheme of dry/wet fronts for the Saint-Venant system of shallow water equations ∙ found at: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.700.7977&rep=rep1&type=pdf ∙ http://visdom.at/media/pdf/publications/Poster.pdf ∙ (last visited 2018-06-29)</ref>
</references>
</references>
}}
{{WaterOverlay formula nav}}

Latest revision as of 16:54, 5 March 2024

The elevation model is determined using two steps:

  • Rasterization of the height sectors and buildings
  • Piecewise linear reconstruction of the bottom

Rasterization of height points of height sectors and buildings

The base land height values can originate from two sources:

Often the height source has more height values for a particular grid cell. The calculate height value for that grid cell is then calculated as the average of these points.

Added to the rasterized land height are the building heights. A building's height is calculated based on the floor height times the amount of floors, slanting roof height and optional height offset. In case a building has a Custom Geometry, the height is calculated based on this custom geometry, within the boundaries of the grid cell, with the addition of the optional height offset.

How bridges are handled as buildings depend on the configured bridge mode.

These buildings heights (including bridges!) are limited by the design flood elevation and the height taken is whichever is lowest.


Furthermore certain conditions, such as a configured Weir Height or Culvert Threshold can override a grid cell elevation. This overriding also provides a preference for the piecewise linear reconstruction.

Piecewise linear reconstruction of the bottom

The implementation of the Water Module is based on second-order semi-discrete central-upwind scheme by Kurganov and Petrova (2007)[1]. The surface elevation, also named bottom in the paper, is slightly adjusted to support the scheme to become well balanced and positivity preserving. The process of adjusting the original surface elevation is called piecewise linear reconstruction of the bottom.

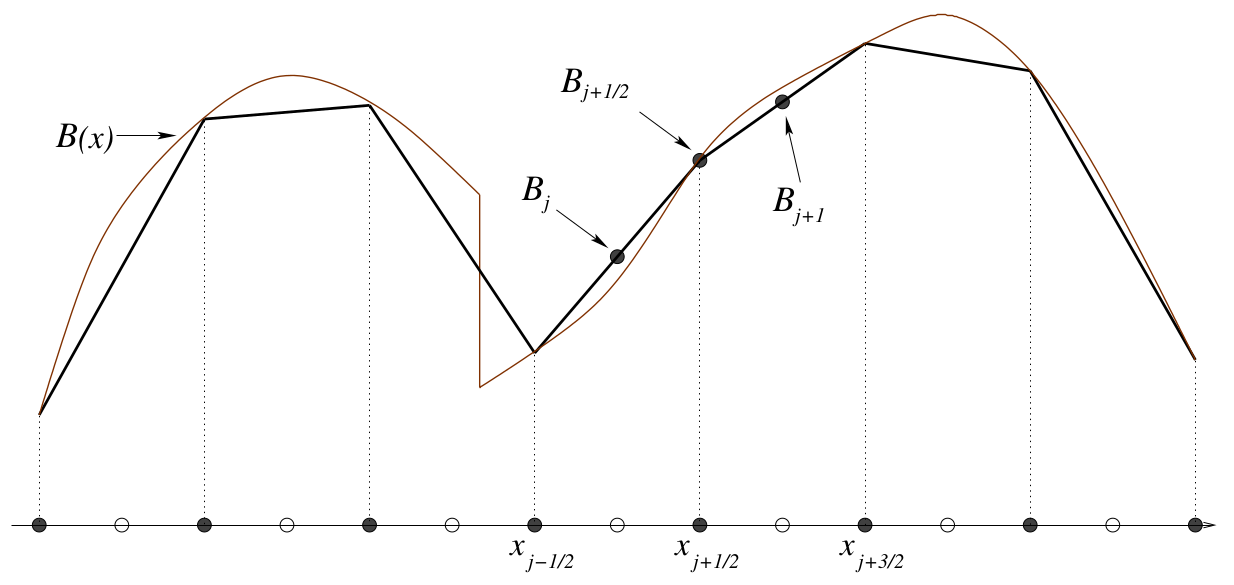
1D linear piecewise reconstruction. Source: Kurganov and Petrova (2007)[1]

The first requirement the scheme to become well balanced and positivity preserving is to ensure that each grid cell has a constant linear slope in both the x- and y- direction. Secondly the end points of the slope should meet in the center of the cell's edges. This ensures that the bottom is continuous along cells in the x- and y- direction. Thirdly, the linear slope in the x- and y-direction within a cell should meet in a single center point.

To fulfill these requirements, the following steps are taken:

  1. Pick or calculate the height points for the 4 corners of the cell. A height point is picked when an override height is provided, such as a Weir Height.
  2. Form a rectangle with the 4 corners and calculate the centers of these edges. (These are the points that have to meet for continuity)
  3. Calculate a new center point based on the 4 edge center points.

Given that the adjacent cells share the same corner points, and thus share an edge center point, the bottom will be continuous in the x and y direction. Furthermore, the cell has an linear slope in both the x- and y-direction. The only downside is that the new center point might have been placed heigher or lower in a situation where the terrain's slope was originally not linear within the cell.

  • 2D linear piecewise reconstruction. Source: Horváth et al. (2014)[2]

  • Application of reconstructed elevation Source: Horváth et al. (2014)[2]

Notes

See also

References

  1. ↑ 1.0 1.1 Kurganov A, Petrova G (2007) ∙ A Second-Order Well-Balanced Positivity Preserving Central-Upwind Scheme for the Saint-Venant System ∙ found at: http://www.math.tamu.edu/~gpetrova/KPSV.pdf (last visited 2018-06-29)
  2. ↑ 2.0 2.1 Zsolt Horváth, Jürgen Waser, Rui A. P. Perdigão, Artem Konev and Günter Blöschl (2014) ∙ A two-dimensional numerical scheme of dry/wet fronts for the Saint-Venant system of shallow water equations ∙ found at: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.700.7977&rep=rep1&type=pdf ∙ http://visdom.at/media/pdf/publications/Poster.pdf ∙ (last visited 2018-06-29)
Water Module
Benchmarks button.png
Introduction button.png
Water Module
Benchmarks button.png
Getting started button.png
Tutorials
Benchmarks button.png
Overview button.png
Overview
Benchmarks button.png
Theory button.png
Theory
Benchmarks button.png
Benchmarks button.png
Benchmarks
Models
Surface • Ground • Rain • Evaporation • Infiltration • Elevation • Breach • Sewer • Storage • Tracer flow • Border • Order
Model formulas
Timestep • Season • Surface water level • Groundwater level
Flow formulas
Surface flow • Surface infiltration • Ground flow • Ground infiltration • Surface evaporation • Ground evaporation • Ground bottom flow
Hydraulic structure formulas
Culvert • Weir • Breach growth • Breach flow • Pump • Sewer Overflow • Inlet • Drainage
Related
Building attributes • Hydrological features • Hydraulic structures •  Terrain attributes • Model attributes • Results • Simulation data
Retrieved from "https://support.tygron.com/w/index.php?title=Elevation_model_(Water_Overlay)&oldid=60199"