Breach growth formula (Water Overlay): Difference between revisions

From Tygron Support wiki
Jump to navigation Jump to search
No edit summary
No edit summary
Line 19: Line 19:
Where:
Where:
: <math>W_b</math> = The [[Breach width (Water Overlay)|BREACH_WIDTH]] of the breach.
: <math>W_b</math> = The [[Breach width (Water Overlay)|BREACH_WIDTH]] of the breach.
: <math>H_{b,t}</math> = The [[Breach height (Water Overlay)|BREACH_HEIGHT]] (datum) of the breach at time t.
: <math>H_{b,t}</math> = The [[Breach height (Water Overlay)|BREACH_HEIGHT]] ({{datum}}) of the breach at time t.
: <math>W_{b,t}</math> = The calculated breach width, initially equal to <math>W_b</math>.
: <math>W_{b,t}</math> = The calculated breach width, initially equal to <math>W_b</math>.
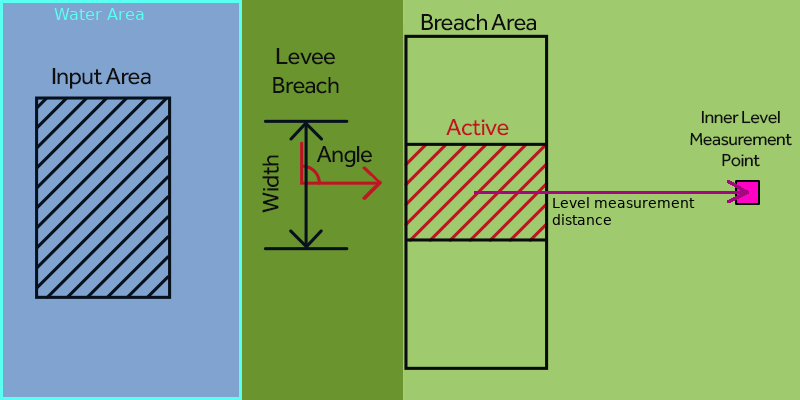
: <math>w_{i,t}</math> = Inner water level at breach area at time t, measured at the [[Breach measurement distance m (Water Overlay)|measurement point]] (or [[Breach level area (Water Overlay)|Level Area]]) of the [[Breach (Water Overlay)|Breach]].
: <math>w_{i,t}</math> = Inner water level at breach area at time t, measured at the [[Breach measurement distance m (Water Overlay)|measurement point]] (or [[Breach level area (Water Overlay)|Level Area]]) of the [[Breach (Water Overlay)|Breach]].

Revision as of 15:40, 25 January 2024

Water can flow through breaches into levee protected areas. These breaches often start small and grow over time.

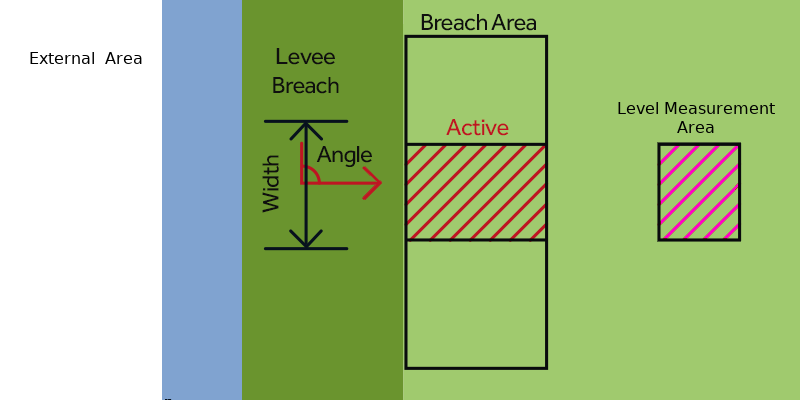
The water flowing through breaches can originate from an external area outside the project area or an input area within the project area.

This algorithm is based on the incremental timestep formula of Verheij-van der Knaap[1], as described in section 3.4.4 Implementatie in SOBEK and the conclusion of that paper.

First, the difference in height of the water on either side of the breach is calculated.

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta h_{t} = \left | w_{o,t} - max(w_{i,t}, H_{b,t}) \right |}

Using the height difference, the breach width increase (m/s) is calculated per computational timestep.

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta W_{b,t} = \frac{f_1 \cdot f_2}{ ln(10)} \cdot \frac{(g \cdot \Delta h_{t})^{1.5 }}{ {cs_b}^2} \cdot \frac{1} { 1 + \frac{f_2 \cdot g \cdot \Delta t} {cs_b \cdot 3600}}}

The current breach width is then equal to the last calculated breach width, plus the calculated breach width increment.

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_{b,t} = W_{b,t-1} + \Delta W_{b,t} \cdot \frac{\Delta t }{ 3600}}

Where:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_b} = The BREACH_WIDTH of the breach.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{b,t}} = The BREACH_HEIGHT (datum) of the breach at time t.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_{b,t}} = The calculated breach width, initially equal to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_b} .
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_{i,t}} = Inner water level at breach area at time t, measured at the measurement point (or Level Area) of the Breach.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_{o,t}} = Outer water level at Input Area (or external area) at time t.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta h_{t}} = The difference between the height of the water columns on either side of the breach at time t.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_1} = Material factor, set to 1.3 (average for sand and clay levees).
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_2} = Constant, set to 0.04.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g} = the acceleration due to gravity, set to 9.80665.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cs_{b}} = The critical BREACH_SPEED of the breach (e.g. 0.2 for sand and 0.5 for clay).
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta W_{b,t}} = The calculated width increase of the breach at time t.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta t} = Computational timestep.


Breach with (internal) Input Area and a Measurement Point
Breach with External Water Level and a Breach Level Area


Notes

  • The breach height Hb,t can be defined over time, by configuring the BREACH_HEIGHT as an attribute array.
  • The inner water level is to be measured not directly inside the breach area but a few meters away. By default 100m, this can be adjusted via the BREACH_MEASUREMENT_DISTANCE_M attribute. It can also be measured using a manual defined level area.
  • For more details on breach growth, we also recommend reading this "Quickscan"-report for Waterschap Rijn en IJssel[2].

How-to's

Related

The following topics are related to this formula.

Features
Breach
Formulas
Breach flow formula
Models
Breach Model
Surface model

See also

For an example of the breach growth, take a look at the Demo Breach Project available in all domains.

References

  1. ↑ Verheij, H.J. ∙ Aanpassen van het bresgroeimodel in HIS-OM: Bureaustudie ∙ found at: http://resolver.tudelft.nl/uuid:aedc8109-da43-4a03-90c3-44f706037774 ∙ (last visited 2022-09-08)
  2. ↑ Arcadis ∙ Quickscan Lijnvormige Kerende Elementen Onderzoek naar de modellering van bresgroei en standzekerheid van Lijnvormige Kerende Elementen Waterschap Rijn en IJssel ∙ found at: https://edepot.wur.nl/556012 ∙ (last visited 2022-09-08)
Water Module
Benchmarks button.png
Introduction button.png
Water Module
Benchmarks button.png
Getting started button.png
Tutorials
Benchmarks button.png
Overview button.png
Overview
Benchmarks button.png
Theory button.png
Theory
Benchmarks button.png
Benchmarks button.png
Benchmarks
Models
Surface • Ground • Rain • Evaporation • Infiltration • Elevation • Breach • Sewer • Storage • Tracer flow • Border • Order
Model formulas
Timestep • Season • Surface water level • Groundwater level
Flow formulas
Surface flow • Surface infiltration • Ground flow • Ground infiltration • Surface evaporation • Ground evaporation • Ground bottom flow
Hydraulic structure formulas
Culvert • Weir • Breach growth • Breach flow • Pump • Sewer Overflow • Inlet • Drainage
Related
Building attributes • Hydrological features • Hydraulic structures •  Terrain attributes • Model attributes • Results • Simulation data
Retrieved from "https://support.tygron.com/w/index.php?title=Breach_growth_formula_(Water_Overlay)&oldid=57513"