Breach flow formula (Water Overlay): Difference between revisions
No edit summary |
|||
| Line 28: | Line 28: | ||
: <math>A_{b}</math> = The (optional) size of the bottom of the entry area; In case of an external area: the second value provided for the [[External area (Water Overlay)|EXTERNAL_AREA]] of the breach. In case only one value is provided, <math>A_{b} = A_{s}</math> | : <math>A_{b}</math> = The (optional) size of the bottom of the entry area; In case of an external area: the second value provided for the [[External area (Water Overlay)|EXTERNAL_AREA]] of the breach. In case only one value is provided, <math>A_{b} = A_{s}</math> | ||
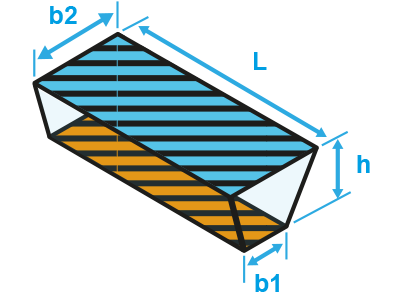
==Trapezoidal prism== | ==Trapezoidal prism== | ||
[[File:external_water_body_trapezoid.png|right|External water body as a trapezoid]] | |||
The [[External area (Water Overlay)|external water area]] can also be represented as a trapezoidal prism. The new water level then has to be calculated differently. | The [[External area (Water Overlay)|external water area]] can also be represented as a trapezoidal prism. The new water level then has to be calculated differently. | ||
Revision as of 15:18, 28 June 2023
Flow through breaches is calculated based on the weir formula, including the consideration between free flow and submerged flow situations. The weir formula is supplied with the breach width (as stand-in for the weir width), which is always calculated with the breach growth formula before calculating the weir flow. The downstream water level can optionally be measured with an additionally configured Breach Level Area, or an automatically placed at a distance based on the configured measurement distance and the orientation of the breach.
For the entry area, the area where the water originates from, the following also applies:
- The water level used is defined by either an input area or the external water level.
- In case of an external area, the surface height used is defined by external surface level. This height limits how far the water level can be lowered.
- Optionally a second value can be supplied for the external surface level. In that case, the second value represents the area of the bottom.
- In case of an input area, the average water level is based on the water level on the individual grid cells of the input area.
Each timestep, the external water level is changed based on the amount of water flowing in or out.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_e = w_{e,t} - z_b}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta V = min(h_e \cdot A_s , Q_{w,t} \cdot \Delta t)}
In case Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_s = A_b} :
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_{e,t+1} = w_{e,t} - \frac{\Delta V}{A_b}}
Where:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_{b}} Datum height of the bottom of the area water flows from.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_{e,t}} = The water level of the entry area at time Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} ; In case of an external area: EXTERNAL_WATER_LEVEL of the breach.
- = The calculated water flow which takes place at time Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} , based on the weir formula.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta t} = The timestep in seconds.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta V} = The limited volume of water transported, based on the remaining water.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{s}} = The size of in the entry area; In case of an external area: EXTERNAL_AREA of the breach.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{b}} = The (optional) size of the bottom of the entry area; In case of an external area: the second value provided for the EXTERNAL_AREA of the breach. In case only one value is provided, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{b} = A_{s}}
Trapezoidal prism
The external water area can also be represented as a trapezoidal prism. The new water level then has to be calculated differently.
The length and width of the surface area are currently considered equal. Therefore:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L = \sqrt{A_s}}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_s = L}
The width of the bottom area is then calculated as:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_b = \frac{A_b}{L}}
Next, we will calculate the new water level based on Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta V} :
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_0 = w_{e,0} - z_b}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a = \frac{W_s-W_b}{4 \cdot h_0}}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{t,t} = 2 \cdot (a \cdot h_t^2 + 0.5 \cdot W_b \cdot h_t)}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta A = \frac{\Delta V}{L}}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c = \frac{-\Delta A * A_{t,t}}{2}}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D = (\frac{W_b}{2})^2 - 4 \cdot a \cdot c}
if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D < 0} , determine the new water level based on a box shape:
otherwise, determine the new water level based on the determinant and flow direction:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_{-} = \frac{-\frac{W_b}{2} - \sqrt{D}}{2 \cdot a} + z_b}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_{+} = \frac{-\frac{W_b}{2} + \sqrt{D}}{2 \cdot a} + z_b}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_{e,t+1} = \begin{cases} w_{+} & \mbox{ if } \Delta V < 0 & \mbox{ and } w_{+} \le w_{e,t}\\ w_{-} & \mbox{ if } \Delta V < 0 & \mbox{ and } w_{+} > w_{e,t}\\ w_{+} & \mbox{ if } \Delta V \ge 0 & \mbox{ and } w_{-} < w_{e,t}\\ w_{-} & \mbox{ if } \Delta V \ge 0 & \mbox{ and } w_{-} \ge w_{e,t}\\ \end{cases} }
Where:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_{b}} = Datum height of the bottom of the area water flows from.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_{e,t}} = The water level of the entry area at time Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} ; In case of an external area: EXTERNAL_WATER_LEVEL of the breach.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q_{w,t}} = The calculated water flow which takes place at time Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} , based on the weir formula.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta t} = The timestep in seconds.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta V} = The limited volume of water transported, based on the remaining water.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{s}} = The size of in the entry area; In case of an external area: EXTERNAL_AREA of the breach.
- = The (optional) size of the bottom of the entry area; In case of an external area: the second value provided for the EXTERNAL_AREA of the breach. In case only one value is provided, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{b} = A_{s}}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} = Length of the trapezoidal prism
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_s} = Width of the original top (surface at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t = 0} ) of the trapezoid
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_b} = Width of the bottom of the trapezoid
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_0} = The initial relative water height in the external area.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} = Slope of the trapezoid
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{t,t}} = Area of the trapezoidal slide of the trapezoid prism at time Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c} = Constant based on new area of the trapezoid Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{t,t+1}}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D} = Polynomial discriminant
Notes
- The water level we cannot become lower than the surface height se, defined by EXTERNAL_SURFACE_LEVEL in case of an external entry area. In case of an input area within the project, the surface height is determined per grid cell.
- When water is flowing from the project area to an external area, the slope of the external area remains the same, even when the water level rises above the original water level. In the case of a trapezoidal prism, is extrapolated upwards.
Related
The following topics are related to this formula.
- Features
- Breach
- Formulas
- Weir formula
- Breach growth formula
- Models
- Surface model