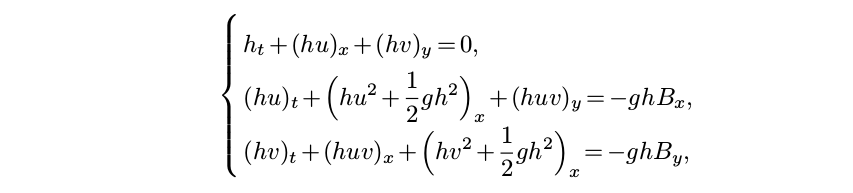Surface model (Water Overlay)
Computation
The Water Module's primary function is simulating two-dimensional flow of water along the surface. In order to do this, the project area is first discretized into x by y cells depending on the configured grid cell size. Secondly, a set of rules is required that describes the behavior of the flow. This is done through a second-order semi-discrete central-upwind scheme produced by Kurganov and Petrova (2007)[1], which is based on the 2-D Saint-Venant equations (a.k.a. shallow water equations):
where
- ht = water depth at time t
- ut = velocity in the x direction at time t
- vt = velocity in the y direction at time t
- Bx = slope in the x direction
- By = slope in the y direction
- g = gravitational constant
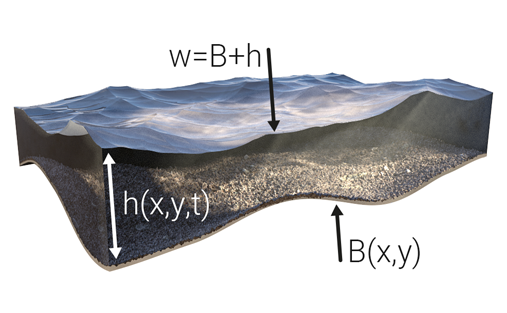
This method deviates from the original Saint-Venant equations in that it approaches the system in terms of water surface elevation (w = h + B) and flux (hu and hv), rather than just the water depth (h). The image on the right aims to clarify on the various terms. More technical information on the Tygron Platform's implementation of the Well-Balanced Positivity Preserving Central-Upwind Scheme can be found here.
Flowing water
Imbalances in the water surface elevation among grid cells drive the flow of water in the model until a state of equilibrium is reached in terms of w and flux.
Water level initialization
In theory, each grid cell can have a unique water level and accompanying water depth. In practice though, water levels are often initialized for large groups of cells, since it is assumed that a particular area within the project area has a given water level. Therefore, the surface water level is initialized based on hydrological features. We make the following distinction:
- Water levels of water terrains.
- Potential water levels for inundated land.
For all water terrains, the amount of water set on the grid cell is such that the resulting water level in that location is equal to the WATER_LEVEL attribute provided by the Water level area. If no water level area is overlapping that grid cell, or the water level is below the surface elevation of the grid cell, the water depth is assumed to be 0 and the water level equal to the surface elevation.
For the second case, inundation areas have been added to the model. Water is placed in all grid cells which are covered by an inundated area, (regardless of the terrain type in that location, in contrast to the water level areas), such that the resulting water level is again equal to the inundation area's INUNDATION_LEVEL attribute. If no inundation area is overlapping that grid cell, or the inundation level is below the surface elevation of the grid cell, the water depth is assumed to be 0 and the water level equal to the surface elevation.
The terrain height is defined by the terrain height in the project. The surface height is further influenced by the height of constructions present in the project (bounded by DESIGN_FLOOD_ELEVATION_M) and by the BREACH_HEIGHT of breaches.
Notes
- Water can be added to and removed from the described surface system by the rain, evaporation and infiltration model, as well as certain hydraulic structures, sewers and breaches.
- Underground flow uses a different flow system and formula's, described in underground model.
- In addition to water flowing between adjacent grid cells, water can also flow through hydraulic constructions.
Related formulas
- Culvert formula
- Weir formula
- Breach growth formula
- Breach flow formula
- Pump formula
- Sewer overflow formula
- Inlet formula
Related models
References
- ↑ Kurganov A, Petrova G (2007) ∙ A Second-Order Well-Balanced Positivity Preserving Central-Upwind Scheme for the Saint-Venant System ∙ found at: http://www.math.tamu.edu/~gpetrova/KPSV.pdf (last visited 2019-04-11)