UK Benchmark 1 (Water Module): Difference between revisions
| Line 27: | Line 27: | ||
* External area (m2): 1 000 000 000; | * External area (m2): 1 000 000 000; | ||
* Water level (m): 1; | * Water level (m): 1; | ||
* Inlet Q (m) : | * Inlet Q (m) : | ||
{| | {| | ||
! time (hrs) | ! time (hrs) | ||
| Line 45: | Line 44: | ||
| -1000 | | -1000 | ||
|} | |} | ||
* Threshold (m): dynamic, see below; | * Threshold (m): dynamic, see below; | ||
The threshold array was set using a .csv-file that approximated there water level over time. It is approximated since our water levels remain the same for a given period of time (no linear interpolation between time key - values). However, this setup proved accurate enough. The ''inletthresholds.csv''-file can be found in the zip-file below. | The threshold array was set using a .csv-file that approximated there water level over time. It is approximated since our water levels remain the same for a given period of time (no linear interpolation between time key - values). However, this setup proved accurate enough. The ''inletthresholds.csv''-file can be found in the zip-file below. | ||
Revision as of 12:29, 17 April 2019
This page contains the test case 1 of the UK benchmark named Test 1 – Uncovering of a beach as well as its result generated by the Water Module in the Tygron Platform.
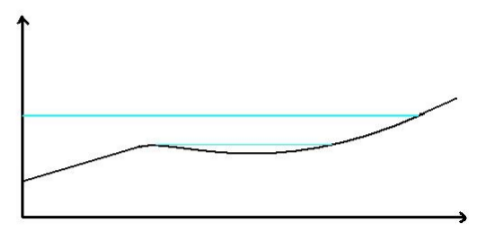
This test consists of a sloping topography with a depression. An inflow boundary condition is applied at the low end, causing the water to rise to the level indicated by a thick blue line. The inflow is then replaced by a sink term until the water level becomes as indicated by the thin blue line. A similar test has been used by EDF (2000) for validation of the TELEMAC package. The aim of the test is to assess basic package capabilities such as handling disconnected water bodies and wetting and drying of floodplains.
Description
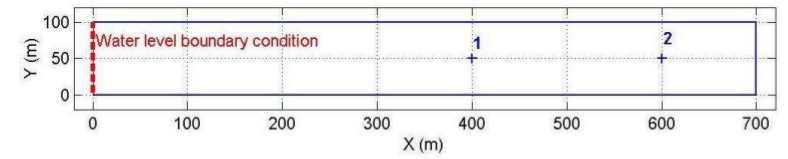
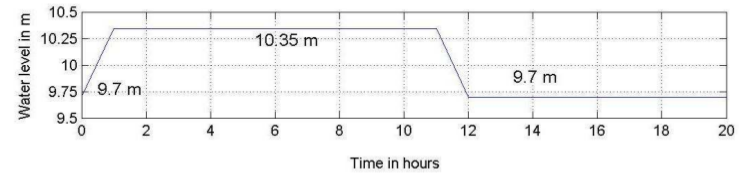
This test consists of a sloping topography with a depression as illustrated in Figure (a). The modeled domain is a perfect 700m x 100m rectangle. A varying water level, see Figure (b), is applied as a boundary condition along the entire length of the left-hand side of the rectangle, causing the water to rise to level 10.35m. This elevation is maintained for long enough for the water to fill the depression and become horizontal over the entire domain. It is then lowered back to its initial state, causing the water level in the pond to become horizontal at the same elevation as the sill, 10.25m.
Boundary and initial conditions
Varying water level along the dashed red line in Figure (a). Table provided as part of dataset. All other boundaries are closed.
Initial condition: Water level elevation = 9.7m.
Parameter values
- Manning’s n: 0.03 (uniform)
- Model grid resolution: 10m (or 700 nodes in the area modelled)
- Time of end: the model is to be run until time t = 20 hours
Technical setup
The provided ascii height file named test1DEM.asc is first imported. It has a cell size of 2m, while the test is expected to run on a 10m grid. Therefore, it will be automatically rescaled by the grid rasterizer. The resulting rescaled asc file is packed in the down below.
In order to regulate the water level according to the water level graph, we used the following setup:
- On gridcells with x = 1 and x = 2 Inlet objects were placed. Each inlet had its own grid cell. The inlets were configured as:
- External area (m2): 1 000 000 000;
- Water level (m): 1;
- Inlet Q (m) :
| time (hrs) | inlet Q (m3/s) |
|---|---|
| 0, | 1000, |
| 11 | 1000 |
| 11 + 1 sec | -1000 |
| 22 | -1000 |
- Threshold (m): dynamic, see below;
The threshold array was set using a .csv-file that approximated there water level over time. It is approximated since our water levels remain the same for a given period of time (no linear interpolation between time key - values). However, this setup proved accurate enough. The inletthresholds.csv-file can be found in the zip-file below.
Output as required
- Software package used: Tygron Platform
- Numerical scheme: FV (Kurganov, Bollerman, Horvath)*
- Specification of hardware used to undertake the simulation:
- Processor: Intel Xeon @2.10GHz x 8,
- RAM 62.8 GiB,
- GPU: 2x NVidia 1080
- Operating system: Linux 4.13
- Time increment used: adaptive: 0.25 - 1.13 s.
- Grid resolution: 10 m.
- Simulation time: 28s.
- Remaining volume water: 18672 m3
Measured point graphs are displayed below:
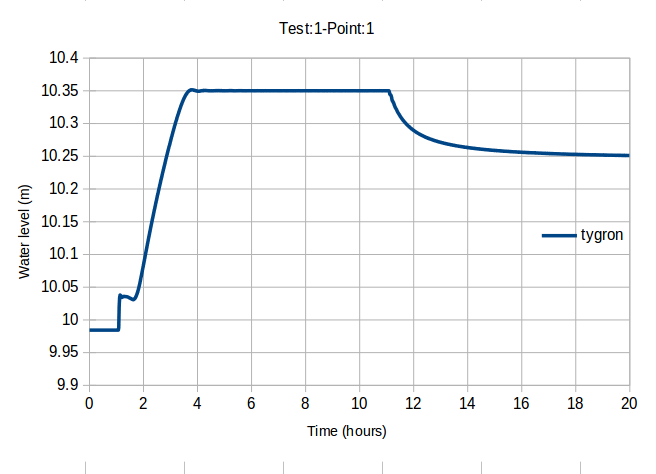
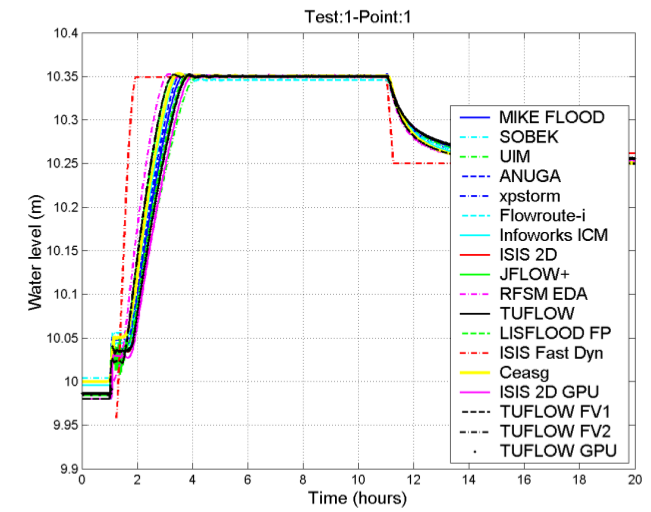
- Graph of point 1 generated by the Tygron Platform on the left and generated by others on the right.
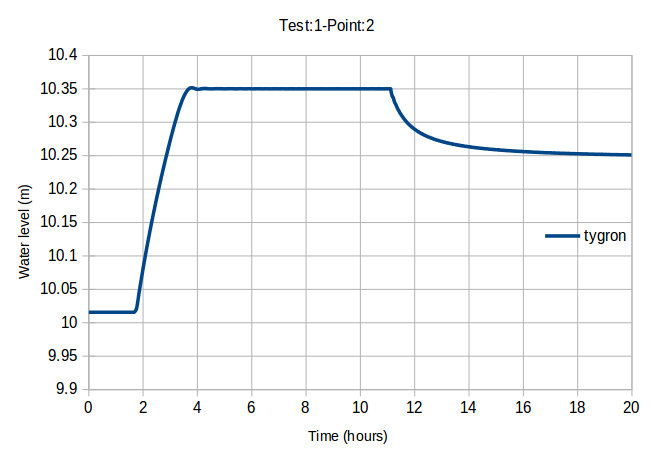
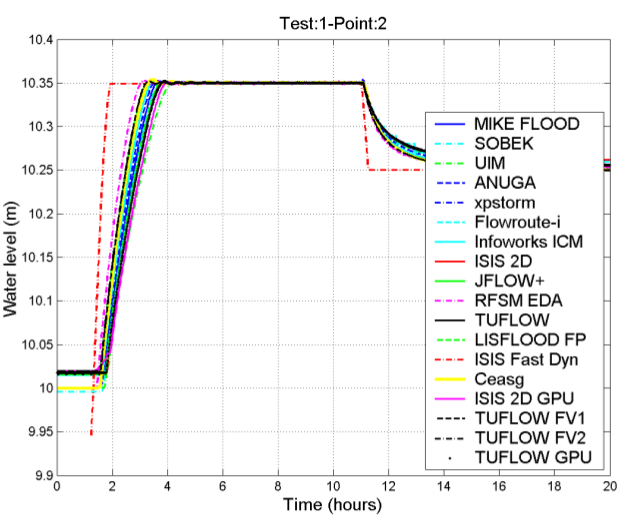
- Graph of point 1 generated by the Tygron Platform on the left and generated by others on the right.
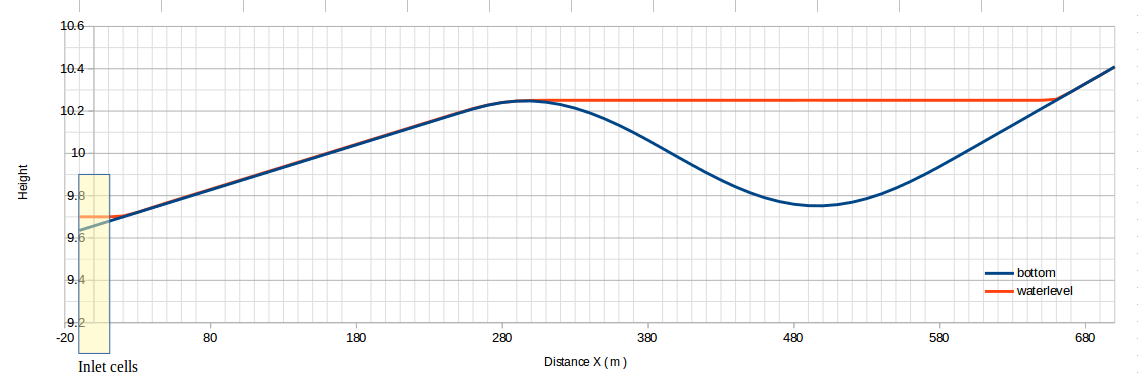
- Slice of the situation in the x -direction, generated by the Tygron Platform.
Notes
- Tests are run with multi gpu setup. For small cases like this, running it on a single gpu is actually faster: 17 seconds, which is +- 40% compared to 2.