Elevation model (Water Overlay): Difference between revisions
Jump to navigation
Jump to search
(Created page with "Two aspects are described on this page: Rasterization of the height sectors Piecewise linear reconstruction of the bottom. ===Piecewise linear reconstruction of the bottom==...") |
|||
| Line 8: | Line 8: | ||
The surface elevation, also named bottom in the paper, is slightly adjusted which allows the scheme to become well balanced and positivity preserving. | The surface elevation, also named bottom in the paper, is slightly adjusted which allows the scheme to become well balanced and positivity preserving. | ||
The process of adjusting the original surface elevation is called ''piecewise linear reconstruction of the bottom''. It works as followed: | The process of adjusting the original surface elevation is called ''piecewise linear reconstruction of the bottom''. It works as followed: | ||
[[File:piecewisereconstruction_1d]] | [[File:piecewisereconstruction_1d.png]] | ||
[[File:Inundation overlay 04 HWP(1).PNG|thumb|250px|Source: Horváth et al. (2014)<ref name="Horvath"/>]] | [[File:Inundation overlay 04 HWP(1).PNG|thumb|250px|Source: Horváth et al. (2014)<ref name="Horvath"/>]] | ||
Revision as of 12:12, 12 April 2019
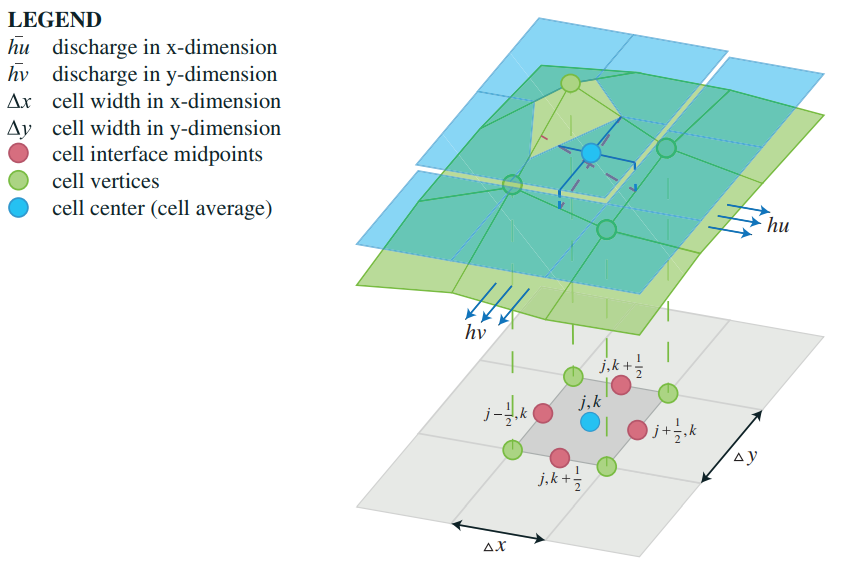
Two aspects are described on this page: Rasterization of the height sectors Piecewise linear reconstruction of the bottom.
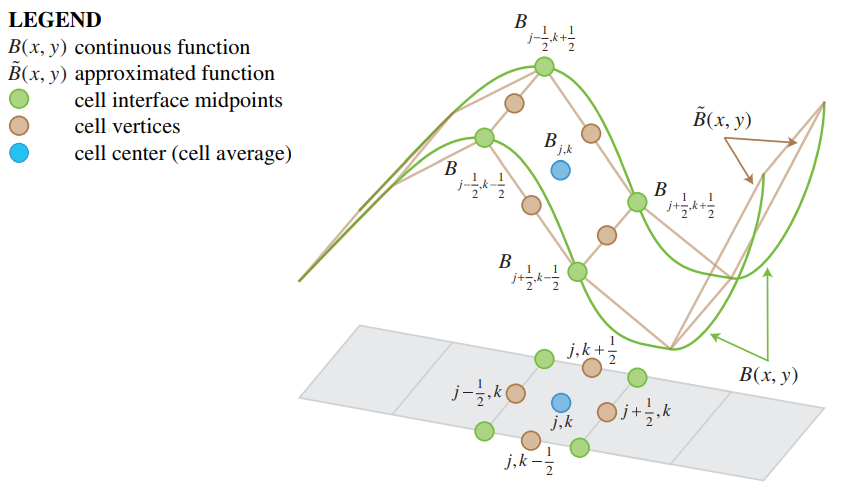
Piecewise linear reconstruction of the bottom
The implementation of the Water Module is based on second-order semi-discrete central-upwind scheme by Kurganov and Petrova (2007)[1]
The surface elevation, also named bottom in the paper, is slightly adjusted which allows the scheme to become well balanced and positivity preserving.
The process of adjusting the original surface elevation is called piecewise linear reconstruction of the bottom. It works as followed:
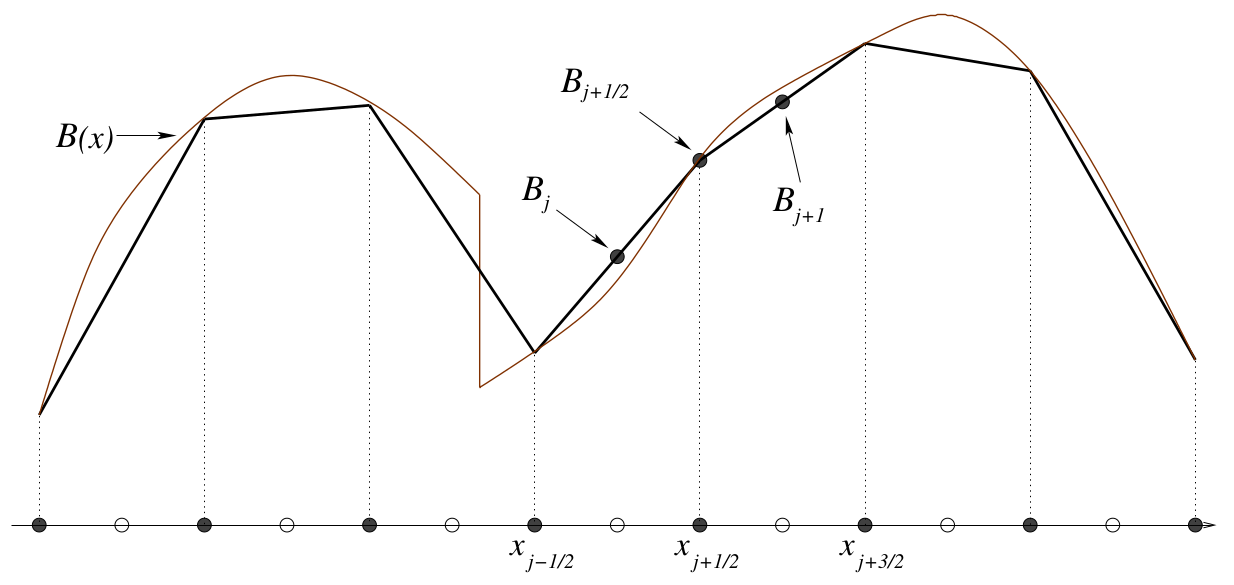

Source: Horváth et al. (2014)[2]

Source: Horváth et al. (2014)[2]
References
- ↑ Kurganov A, Petrova G (2007) ∙ A Second-Order Well-Balanced Positivity Preserving Central-Upwind Scheme for the Saint-Venant System ∙ found at: http://www.math.tamu.edu/~gpetrova/KPSV.pdf (last visited 2018-06-29)
- ↑ 2.0 2.1 Zsolt Horváth, Jürgen Waser, Rui A. P. Perdigão, Artem Konev and Günter Blöschl (2014) ∙ A two-dimensional numerical scheme of dry/wet fronts for the Saint-Venant system of shallow water equations ∙ found at: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.700.7977&rep=rep1&type=pdf ∙ http://visdom.at/media/pdf/publications/Poster.pdf ∙ (last visited 2018-06-29)