Wind calculation model (Heat Overlay)

The wind speed on streetlevel (1.2 meter) is calculated using a translation of the 10 meter wind speed measured at a weather station. A single reduction field per wind direction can be calculated, which in turn can be multiplied with the 10 meter wind speed to obtain the wind speed at streetlevel. The calculation model is based on the McDonald (2000) method for wind in cities. It uses the vertical surfaces of buildings perpendicular to the wind direction to determine in what way the wind speed is slowed down. The DPRA Heat stress report has extended this method with perpendicular vertical tree surfaces as well.

Implementation

Our implementation differs slightly from the implementation described by DPRA Heat stress report. It does not do cubic interpolation from coarse grids to more detailed grids. We do all operations on a detailed grid.

Our implementation is as followed:

Average window

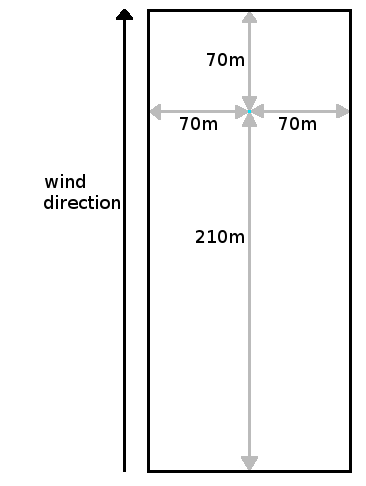
First of all, the wind window has to be selected. If the wind speed is lower than 1.5 m/s, a window of 175 by 175 is used for averaging. Else a window of 140x280 is taken. See the image below:

Per grid cell

Per wind window grid cell:

1. Determine the average obstacle height per square meter. Buildings and trees lower than 2 meters are not taken into account. It is divided by the area of the search window.
2. Determine the average vertical building surface perpendicular to the wind direction. Again this is divided by the area of the search window.
3. Determine the frontal surface compactness factor $\lambda$, separately for buildings and trees. Combine these to obtain $\lambda _{cor}$.
4. Determine the average height of trees, with 4 meters as minimum value.
5. Using these values, select the correct formula parameters from the McDonald 2000 table for $d$, $z_{w}$, $z_{0}$, $A$ and $B$
6. Using the obtained parameters, calculate the wind translation factor.
7. Obtain the wind speed at $u_{1,2}$ by multiplying the wind translation factor with the $u_{10}$ measured at the weather station. Since the wind speed can still be too low, apply a correction formula to $u_{1,2}$ to obtain the end result.

Step 2

For each strip in the direction of the wind: Check if the height of buildings is higher than the previous cell:

  if $H_{curr}>H_{prev}$ and $H>2.0$
     $S_{frontal}=S_{frontal}+(H_{curr}-H_{prev})\cdot w_{cell}$
  $H_{prev}=H_{curr}$

where $w_{cell}$ is the width of a cell. So we only calculate additional heights.

Next, divide $S_{frontal}</mathbytheamountofcellsvisited.==Step3==First,calculate<math>\lambda _{buildings}$ and $\lambda _{foliage}$ in a similar way, described in step 2.

Next, calculate the $\lambda _{cor}$ using the $\lambda _{buildings}$ and $\lambda _{foliage}$.

$\lambda _{cor}=0.6\cdot \lambda _{buildings}+0.3\cdot \lambda _{foliage}+0.015$.

Step 4

Calculate the average obstacle height $H$, where a minimum height threshold of 4 is used. This means it is always at least 4 meters high.

Step 5

Select the function parameters $d$, $z_{w}$, $z_{0}$, $A$ and $B$ from the table using $H$ and $\lambda _{cor}$:

$\lambda _{cor}$	${\frac {d}{H}}$	${\frac {z_{w}}{H}}$	${\frac {z_{0}}{H}}$	${\frac {A}{H}}$	$B$
0.05 (<0.08)	0.066	2	0.048	-0.35	0.56
0.11 (<0.135)	0.26	2.5	0.071	-0.35	0.50
0.16 (<0.18)	0.32	2.7	0.084	-0.34	0.48
0.20 (<0.265)	0.47	1.5	0.08	-0.56	0.66
0.33 (>=0.265)	0.57	1.2	0.077	-0.85	0.92

Step 6

Calculate the translated intermediate wind speeds:

$u_{zw}=u_{60}\cdot {\frac {\ln({\frac {z_{w}-d}{z_{0}}})}{\ln({\frac {60-d}{z_{0}}})}}$

$u^{*}=0.4\cdot {\frac {u_{60}}{\ln({\frac {60-d}{z_{0}}})}}$

$u_{H}={\frac {-u^{*}}{B}}\ln {\frac {A+B_{zw}}{A+B_{H}}}+U_{zw}$

$u_{1.2}=u_{H}\exp(9.8\cdot \lambda \cdot ({\frac {1.2}{H}}-1))$

Step 7

The obtained wind speed $u_{1.2}$ can be too low. Therefore it is corrected with the following formula:

$u_{1.2corr}=u_{10}\cdot ((u_{1.2}-0.0796)\cdot 0.9175+0.1254)$

This corrected value is used in the formula for PET.

---

Heat Module

Heat Module

Tutorials

Overview

Theory

Benchmarks

Group

Calculation models and formulas

Formulas

UHI • Temperatures • Diffuse radiation • PET

Calculation models

Foliage height • Sky view factor • Shade • Average vegetation and sky view factor

Related

Calculation models and formulas • Feature attributes • Model attributes • Result types